INTRODUCCIÓN A LA ESTADISTICA
¡ Bienvenido seas!
Este es un blog que esta organizado que esta hecho para disipar pequeñas dudas que podrías llegar a tener a lo largo de tu cursamiento en la materia de Probabilidad y Estadística.
Sabemos que no es una materia particularmente sencilla, pero la finalidad de este blog es ayudar a la mayor cantidad de personas que necesiten de ayuda en su estudio.
En todo este blog encontraras herramientas que esperamos sean de utilidad para ti, mucha suerte y espero que encuentres lo que buscas.
✌
La Estadística Es la ciencia y el arte de dar sentido a los datos, proporcionando la teoría y los métodos para extraer información Diamond State estos y poder resolver problemas del mundo real. La Estadística trabaja con la incertidumbre se relaciona con otras disciplinas como la medicina, la economía, la agricultura, los negocios, las ingenierías, las ciencias sociales y humanas, entre otras.
Actualmente es usada alrededor del mundo para apoyar la toma de decisiones dentro de
Gobiernos.
Partidos políticos.
Compañías financieras.
Empresas de opinión pública.
Compañías de seguros.
Bancos, hospitales.
Organizaciones sociales e industrias.
Existen cálculos matemáticos que permiten extraer de los datos una tendencia real positiva o negativa de los resultados. Es precisamente la estadística descriptiva la que nos ayuda a analizar y describir los datos para obtener un resultado final.
Estadística descriptiva
El término “estadística descriptiva” se refiere al análisis, el resumen y la presentación de los resultados relacionados con un conjunto de datos derivados de una muestra o de toda la población.
La estadística descriptiva comprende tres categorías principales: distribución de frecuencias, medidas de tendencia central y medidas de variabilidad.
Tipos de estadísticas descriptivas
La estadística descriptiva ayuda a describir y comprender las características de un conjunto de datos específico ofreciendo breves resúmenes sobre la muestra y las medidas de los datos.
Estos son los tipos de estadísticas descriptivas:
Distribución de frecuencias
La distribución de frecuencias es básicamente una presentación o un resumen de datos agrupados que se han clasificado en función de clases mutuamente excluyentes y del número de ocurrencias en cada clase respectiva. Permite una forma más estructurada y organizada de presentar los datos en bruto.
Utilizada tanto para datos cualitativos y cuantitativos. Representa la frecuencia o el recuento de los diferentes resultados en un conjunto de datos o muestra.
Tendencia central
La tendencia central es otro de los tipos de estadística descriptiva, y se refiere al resumen descriptivo de un conjunto de datos utilizando un único valor que refleja el centro de la distribución de los datos. Las medidas de tendencia central también se conocen como medidas de localización central. La media, la mediana y la moda son consideradas las medidas de tendencia central.
La media que se considera la medida de tendencia central más popular, es el valor medio o más común en un conjunto de datos; se divide en dos:
• Media muestral: Es el valor promedio de todas las observaciones del conjunto de datos.
• Media Poblacional: Es el calculo del valor promedio de todas las observaciones de una población.
La mediana se refiere a la puntuación media de un conjunto de datos en orden ascendente; se divide en dos:
Mediana impar: corresponde al valor central de dicho conjunto de datos.
Mediana par: corresponde al promedio de los dos valores centrales (los valores centrales se suman y se dividen entre dos).
La moda se refiere a la puntuación o valor más frecuente en un conjunto de datos.
Variabilidad
Una medida de variabilidad es una estadística de resumen que refleja el grado de dispersión de una muestra. Las medidas de variabilidad determinan la distancia que los puntos de datos parecen tener con respecto al centro.
La dispersión y la variabilidad se refieren y denotan el rango y la amplitud de la distribución de los valores en un conjunto de datos. El rango, la desviación estándar y la varianza se utilizan, respectivamente, para representar diferentes componentes y aspectos de la dispersión.
Medidas de dispersión
las medidas de dispersión son números que indican si una variable se mueve mucho, poco, más o menos que otra. La razón de ser de este tipo de medidas es conocer de manera resumida una característica de la variable estudiada.
Video
Principales medidas de dispersión
Las medidas de dispersión más conocidas son: el rango, la varianza, la desviación típica y el coeficiente de variación (no confundir con coeficiente de determinación). A continuación, veremos estas cuatro medidas.
Rango
El rango es un valor numérico que indica la diferencia entre el valor máximo y el mínimo de una población o muestra estadística. Su fórmula es:
R = Máxx – Mínx
Donde:
R → Es el rango.
Máx. → Es el valor máximo de la muestra o población.
Mín. → Es el valor mínimo de la muestra o población estadística.
x → Es la variable sobre la que se pretende calcular esta medida.
Varianza
La varianza es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su media. Formalmente se calcula como la suma de los residuos al cuadrado divididos entre el total de observaciones. Su fórmula es la siguiente:
Varianza Formula
X → Variable sobre la que se pretenden calcular la varianza
xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Desviación típica
La desviación típica es otra medida que ofrece información de la dispersión respecto a la media. Su cálculo es exactamente el mismo que la varianza, pero realizando la raíz cuadrada de su resultado. Es decir, la desviación típica es la raíz cuadrada de la varianza.
Formula Desviación Típica
X → Variable sobre la que se pretenden calcular la varianza
xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
N → Número de observaciones.
x̄ → Es la media de la variable X.
Coeficiente de variación
Su cálculo se obtiene de dividir la desviación típica entre el valor absoluto de la media del conjunto y por lo general se expresa en porcentaje para su mejor comprensión.
Coeficiente De Variación
X → Variable sobre la que se pretenden calcular la varianza
σx → Desviación típica de la variable X.
| x̄ | → Es la media de la variable X en valor absoluto con x̄ ≠ 0

Variable cualitativa: Hace referencia a una cualidad. Ejemplos: el color de ojos de una persona o el color de pelo.
Se divide en dos, ordinal y nominal:
· Ordinal: tiene un orden predeterminado. Ejemplo nivel de educación.
· Nominal: No tiene un orden predeterminado. Ejemplo sexo, ocupación.
Video
Se dividen en continua y discreta:
· Continua: pueden tomar cualquier valor en un intervalo dado (procesos de medición). Ejemplo: Ingreso, talla peso, etc.
· Discreta: Toma solo ciertos valores (procesos de contar) ejemplo: Número de trabajadores, alumnos, etc.
Importancia de la estadística descriptiva
La estadística descriptiva facilita la visualización de los datos. Permiten presentarlos de forma significativa y comprensible, lo que a su vez da pie a una interpretación simplificada del conjunto de datos en cuestión.
Estadística inferencial
Se llama estadística inferencial o inferencia estadística a la rama de la Estadística encargada de hacer deducciones, es decir, inferir propiedades, conclusiones y tendencias, a partir de una muestra del conjunto. Su papel es interpretar, hacer proyecciones y comparaciones.
Es sumamente útil en el análisis de poblaciones y tendencias, para hacerse una idea posible de las acciones y reacciones de la misma de cara a condiciones específicas. Esto no significa que se las pueda predecir fielmente, ni que estemos en presencia de una ciencia exacta, pero sí de una aproximación posible al resultado final.
Video
población: Una población es un conjunto de elementos o eventos similares que son de interés para alguna pregunta o experimento.
Muestra: Una muestra es un subconjunto de casos o individuos de una población. En diversas aplicaciones, interesa que una muestra sea representativa.
Variables: Se llama a una característica que se observa en una población o muestra. Las variables pueden tomar diferentes valores dependiendo de cada individuo.
Distribución de frecuencias
La distribución de frecuencias es la agrupación de datos en categorías mutuamente excluyentes que indican el número de observaciones en cada categoría. Esto proporciona un valor añadido a la agrupación de datos.
Tablas de frecuencia
• Es la ordenación de la información obtenida de una muestra, en el estudio de una sola variable. El objetivo es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.
Frecuencia absoluta:
• La frecuencia absoluta o simplemente frecuencia es el número de veces que aparece un determinado valor en un estudio estadístico.
Frecuencia acumulada
• Frecuencia acumulada: se obtiene sumando la frecuencia de una clase con la frecuencia acumulada anterior. La primera de todas las frecuencias coincide con la del intervalo en cuestión, y la última es el número total de datos.
Frecuencia relativa
• Frecuencia relativa: se calcula dividiendo la frecuencia absoluta de cada clase entre el número total de datos. Y si se multiplica por 100 se tiene la frecuencia relativa porcentual.
Frecuencia relativa acumulada
• Frecuencia relativa acumulada: es la suma de las frecuencias relativas de cada clase con el acumulado anterior. La última de las frecuencias relativas acumuladas debe ser igual a 1.
Video
Datos agrupados
Los datos agrupados son aquellos que se han clasificado en categorías o clases, tomando como criterio su frecuencia. Esto se hace con la finalidad de simplificar el manejo de grandes cantidades de datos y establecer sus tendencias.
Modelo probabilístico
Un modelo probabilístico o estadístico es la forma que pueden tomar un conjunto de datos obtenidos de muestreos de otros datos con comportamiento que se supone aleatorio.
Frecuencia acumulada
• Frecuencia acumulada: se obtiene sumando la frecuencia de una clase con la frecuencia acumulada anterior. La primera de todas las frecuencias coincide con la del intervalo en cuestión, y la última es el número total de datos.
Frecuencia relativa
• Frecuencia relativa: se calcula dividiendo la frecuencia absoluta de cada clase entre el número total de datos. Y si se multiplica por 100 se tiene la frecuencia relativa porcentual.
Frecuencia relativa acumulada
• Frecuencia relativa acumulada: es la suma de las frecuencias relativas de cada clase con el acumulado anterior. La última de las frecuencias relativas acumuladas debe ser igual a 1.
Modelos de probabilidad discretos: Ensayos de Bernoulli y distribución Binomial.
· La distribución de Bernoulli es un modelo teórico utilizado para representar una variable aleatoria discreta la cual solo puede resultar en dos sucesos mutuamente excluyentes
· Una distribución binomial es una distribución discreta que modela el número de eventos en un número de ensayos fijo. Cada ensayo tiene dos resultados posibles, y evento es el resultado de interés en un ensayo.
Espacio muestral
El espacio muestral o espacio de muestreo (denotado E, S, Ω o U) consiste en el conjunto de todos los posibles resultados de un experimento aleatorio, junto con una estructura sobre el mismo (ver más adelante).
· Por ejemplo, si el experimento consiste en lanzar dos monedas, el espacio muestral es el conjunto (cara, cara), (cara, cruz), (cruz, cara) y (cruz, cruz).
Frecuencia relativa acumulada
• Frecuencia relativa acumulada: es la suma de las frecuencias relativas de cada clase con el acumulado anterior. La última de las frecuencias relativas acumuladas debe ser igual a 1.
Tipo de espacio muestral
Podemos diferenciar entre dos tipos de espacios muestrales: discretos y continuos. Son aquellos espacios donde el número de sucesos elementales es finito o infinito numerable.
· El espacio muestral (S), puede ser discreto o continuo. Es discreto cuando contiene un número finito de puntos o un número infinito numerable 3 de puntos. Así, por ejemplo, en el lanzamiento de un dado, una vez, el espacio muestral S es = {1, 2, 3, 4, 5, 6}, que es un espacio con número finito de puntos.
· El espacio muestral S es continuo si contiene un número infinito no numerable de puntos.
Experimento aleatorio
Experimento aleatorio es la reproducción controlada de un fenómeno, existiendo incertidumbre sobre el resultado que se obtendrá. es aquél en el que si lo repetimos con las mismas condiciones iniciales no garantiza los mismos resultados. Así, por ejemplo, al lanzar una moneda no sabemos si saldrá cara o cruz, al lanzar un dado no sabemos qué número aparecerá, la extracción de las bolas de sorteos, loterías, etc. son experiencias que consideramos aleatorias puesto que en ellas no podemos predecir los resultados las frecuencias relativas acumuladas debe ser igual a 1.
Permutación
Es una técnica de conteo que permite calcular las posibles ordenaciones de los elementos de un conjunto o número de elementos del espacio muestral de un experimento aleatorio. En esta técnica de conteo se considera que existe el orden en la muestra, pero no es posible repetir ningún elemento de la población en su conformación.
Dado un experimento aleatorio con una población N y una muestra n, si en la muestra existe orden, pero no repetición, el número de elementos del espacio muestral corresponde a la permutación de n en N, la cual se simboliza NPn y se define como:
Video
Combinación
Las combinaciones son agrupaciones en las que el contenido importa, pero el orden no. Dos eventos son dependientes si el estado original de la situación cambia de un evento al otro, y esto altera la probabilidad del segundo evento.
Video
Diferencia de combinación y permutación
Las permutaciones son agrupaciones en las que importa el orden de los objetos. Las combinaciones son agrupaciones en las que el contenido importa, pero el orden no. Dos eventos son dependientes si el estado original de la situación cambia de un evento al otro, y esto altera la probabilidad del segundo evento.
Video
Técnicas de conteo
Las técnicas de conteo como el diagrama de árbol, las combinaciones o permutaciones son fórmulas y procesos matemáticos que nos permiten determinar el total de resultados posibles en un evento o experimento, sin embargo, es importante identificar la técnica correcta.
Diagrama de árbol
Es una herramienta de calidad que a través de un proceso sistemático nos permite hallar la relación existente entre un concepto general y los elementos que lo componen.
Dentro de las características de diagrama de árbol tenemos que:
· Permite visualizar la relación entre una generalidad y sus detalles.
· Logramos encontrar causa raíz del problema o situación que se aborda.
· Logramos detectar elementos faltantes (ramas) al tener una visión en conjunto del elemento central.
· Para analizar procesos de forma detallada.
· Como herramienta comunicativa y visual al mostrar la relación entre conceptos de forma gráfica.
· Su elaboración se apoya en otras técnicas y herramientas como tormenta de ideas, diagrama de afinidad y diagrama de relaciones.
Factorial de un numero
La factorial de un número entero positivo se define como el producto de todos los números naturales anteriores o iguales a él.
Video
Experimento de conjunto
Es cualquier proceso que proporciona datos, numéricos o no.
Conjunto.
Un conjunto cuyos elementos representan todos los posibles resultados de un experimento se llama espacio muestral y se representa como S. El espacio muestral de un experimento siempre existe y no es necesariamente único pues, dependiendo de nuestra valoración de los resultados, podemos construir diferentes espacios muestrales.
Conjunto universo
Es el conjunto formado por todos los objetos de estudio en un contexto dado. Se denota por U y también se le llama conjunto universo.
Si en un estudio intervienen los conjuntos A={a, b, c}, B={f, g, h, i, j} y C={x, y}, entonces el conjunto universal U del contexto es:
U= {a, b, c, f, g, h, i, j, x, y}
Es claro que los conjuntos A, B y C son subconjuntos del conjunto universal U: A ⊂ U, B ⊂ U y, C ⊂ U.
Video
Conjunto finito
Son aquellos cuya cardinalidad, o número de elementos de contiene, es igual a un número natural. Un conjunto finito, en otras palabras, es aquel que posee un número de elementos que pueden contarse.
Cardinalidad de un conjunto
Se define como su clase de equivalencia bajo la equipotencial. Se designa un conjunto representativo para cada clase de equivalencia. La elección más habitual es el ordinal inicial en dicha clase.
Video
Distribución de probabilidad
Es como una lista que nos proporciona todos los resultados de los valores que pueden presentarse en un acontecimiento.
Variable aleatoria discreta
Variable aleatoria
· Una variable aleatoria es una función que asigna un valor numérico, al resultado de un experimento aleatorio. Recordemos que el resultado de un experimento aleatorio depende del azar. Espacio muestral discreto.
· Las variables aleatorias discretas son aquellas que presentan un número contable de valores; por ejemplo, el número de personas que viven en una casa (pueden ser 3, 5 o 9).
Video
Distribución binominal
Es una probabilidad discreta y se presenta con mucha frecuencia en nuestra vida cotidiana. Fue propuesta por Jakob Bernoulli (1654-1705), y es utilizada con acontecimientos que tengan respuesta binaria, generalmente clasificada como “éxito” o “fracaso”. Algunos ejemplos donde se aplica esta distribución son:
· Si una persona presenta o no una enfermedad.
· Si una mujer se encuentra en estado de embarazo.
· Que un producto sea exitoso o no.
· Que un vuelo se retrase o no.
· Si el lanzamiento de una moneda sale cara en vez de sello.
· Desigualdades
Video
Distribución de poisson
Recibe su nombre gracias al matemático francés Simeón Denis Poisson (1781-1840). Describe el número de veces que se presenta un acontecimiento durante un intervalo específico, este intervalo puede ser de tiempo, distancia, área o volumen. La probabilidad de ocurrencia es proporcional a la longitud del intervalo. Algunos ejemplos donde se aplica esta distribución son:
· El número de vehículos que vende por día un concesionario.
· Cantidad de llamadas por hora que recibe una compañía.
· Cuando se requiere conocer el número de defectos en un lote de tela.
· Número de accidentes automovilísticos en el año.
· Número de llegadas de embarcaciones a un puerto por día.
· Desigualdades
Video
Modelo probabilístico
Un modelo estadístico es un tipo de modelo matemático que usa la probabilidad, y que incluye un conjunto de asunciones sobre la generación de algunos datos muestrearles, de tal manera que asemejen a los datos de una población mayor.
Distribución
Hipergeométrica
La distribución hipergeométrica
es una distribución de probabilidad discreta relacionada con muestreos
aleatorios y sin reemplazo.
Video
Distribución normal
La distribución normal adapta una
variable aleatoria a una función que depende de la media y la desviación
típica. Es decir, la función y la variable aleatoria tendrán la misma
representación, pero con ligeras diferencias.
Una variable aleatoria continua
puede tomar cualquier número real. Por ejemplo, las rentabilidades de las
acciones, los resultados de un examen, el coeficiente de inteligencia IQ y los
errores estándar son variables aleatorias continuas.


Video
Estimación puntual
·
Una estimación
puntual consiste en establecer un valor concreto (es decir, un punto) para el parámetro.
El valor que escogemos para decir “el parámetro que nos preocupa vale X” es el
que suministra un estadístico concreto. Como ese estadístico sirve para hacer
esa estimación, en lugar de estadístico suele llamársele estimador. Así, por
ejemplo, utilizamos el estadístico “media aritmética de la muestra” como
estimador del parámetro “media aritmética de la población”. Esto significa: si
quieres conocer cuál es el valor de la media en la población, estimaremos que
es exactamente el mismo que en la muestra que hemos manejado.
Video
Población
·
Conjunto homogéneo de
individuos sobre los que se estudian características observables con el
objetivo de extraer alguna conclusión. Por abuso de notación, en ocasiones nos
referimos a la distribución que sigue la variable de interés en vez de al
conjunto de individuos. Así, se dice que estamos ante una población Normal
indicando que la variable que nos interesa sigue una distribución normal.
Parámetro
·
Característica de la
población, como la media y la varianza (o desviación típica) en la distribución
Normal o la probabilidad de éxito en la Binomial son parámetros. Si conocemos
su valor (o si somos capaces de aproximarlo con suficiente precisión) podremos
responder a cualquier pregunta sobre la distribución.
Estadístico
·
cualquier función de
la muestra. Por ejemplo, la media o la varianza muestrales son estadísticos
Estimadores
Son estadísticos independientes
de los parámetros de la población, y que se utilizan para aproximarlos. Si θ es
el parámetro de interés, el estimador se denotará por ˆθ. En el caso de una
población Normal, podemos considerar la media muestral como estimador de la
media poblacional (es decir, X = µˆ) y la varianza muestral como estimador de la
varianza poblacional (s2 = σˆ2). Para una distribución Bi(m, p), donde m denota
el número de pruebas de Bernoulli, la proporción p se puede estimar a partir de
la proporción poblacional (que denotaremos por pˆ). Por tanto, X, s 2 y pˆ son
estimadores puntuales de µ, σ 2 (en distribución Normal) y p (en distribución
Binomial), respectivamente.
Video
Método de muestreo
·
Procedimiento para
seleccionar una muestra. Si en una población queremos obtener una muestra de un
cierto tamaño n (siendo n menor que el tamaño de la población), la manera de
obtener esta muestra no es única. En este tema, consideraremos muestras aleatorias
simples (m.a.s.).
Video
Espero te haya sido de utilidad este blog para adentrarte a la probabilidad y estadística, pronto nos veremos con mas información, hasta pronto internautas.
Websites
donde con la que se completó información:
https://sites.google.com/site/estadisvictoreduc/home/unidad-ii-contenidos-basicos-de-probabilidad/2---espacio-neutralo-espacio-de-eventos
https://virtual.uptc.edu.co/ova/estadistica/docs/1/8.htm#:~:text=El%20espacio%20muestral%20S%20puede,con%20n%C3%BAmero%20finito%20de%20puntos.
https://danacaweb.com/permutaciones.html
https://www.ingenioempresa.com/diagrama-de-arbol/
https://www.sangakoo.com/es/temas/cardinalidad-de-conjuntos
https://www.pragma.com.co/blog/que-es-la-distribucion-de-probabilidad
https://www.pragma.com.co/blog/que-es-la-distribucion-de-probabilidad
https://economipedia.com/definiciones/estadistica-descriptiva.html
https://economipedia.com/definiciones/medidas-de-dispersion.html
Fuente: https://concepto.de/estadistica-inferencial/#ixzz7PhuFbsNS
https://www.universoformulas.com/estadistica/descriptiva/
https://es.slideshare.net/mustrart/modelo-probabilistico-28902911
https://facultad.pucp.edu.pe/ingenieria/carreras/ciencias-estadisticas/que-es-la-estadistica/
Silvia de la Cruz
Homero Rodriguez Gutierrez
Carlos Alberto Ruiz Bustillos
Universidad politécnica de chihuahua










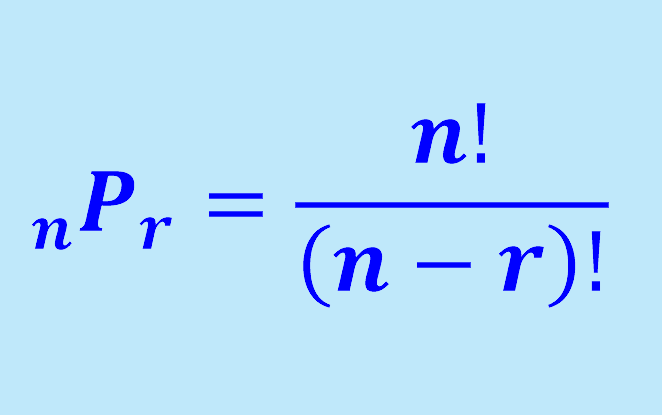
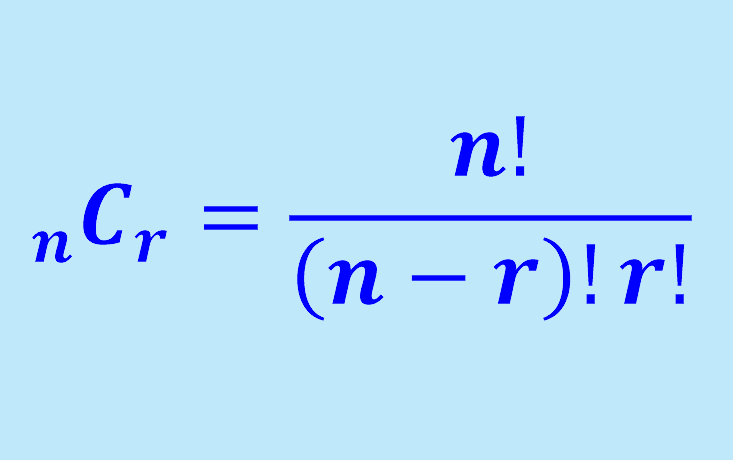








Comentarios
Publicar un comentario